背景

​ 大模型推理的瓶颈主要在于内存带宽，量化是比较好的解决办法，其中模型参数以较低的精度存储，而不是用于训练的典型 16 或 32 位精度。而且证明LLM模型可以以8位精度存储而不会降低性能，其中8位量化不仅将存储要求提高了一半，而且还有可能提高性能推理延迟和吞吐量。

​ 相比较于GPTQ，它使用免训练量化技术，为具有超过数百亿个参数的 LLM 模型实现近乎无损的 4 位量化。然而，实现高量化性能仍然具有挑战性，特别是对于较低位精度和相对较小的模型（例如，< 50B 参数）。

SqueezeLLM: Dense-and-Sparse Quantization | PDF

主要工作

  • 基于Sensitivity的非线性量化
     因为LLM权重分布表现出明显的不均匀模式，之前的推理计算并未完全受益于统一量化，因为算术是以 FP16 精度执行的（W？A16），而不是以降精度执行的（W？A？）非线性量化不支持用于计算加速的整数运算，但这个缺点对于内存限制问题并不重要，因为主要瓶颈在于内存带宽而不是计算。
  • 提出混合量化
     将异常值（Sparse 部分）保存为fp16，其他（Dense部分）保存为低bit值，这样在低bit下更好量化

方法

基于Sensitivity的非线性量化

寻找最佳非均匀量化配置可转化为解决 k-means 问题，给定权重分布，目标是确定最能代表分布的 k 个中心点，

比如3bit量化，$k = 8$ ，可以表示为：
$$
Q(w)^* = \arg \min_Q | W - W_Q |_2^2
$$
虽然这已经优于均匀量化，下面是改进的基于Sensitivity的聚类算法。

量化目标是以低比特精度表示模型权重，同时将模型输出的扰动降至最低，虽然量化会对每一层产生扰动，但我们需要尽量减少整体扰动，因为它能更直接地衡量量化后端到端性能的下降情况。为此，我们需要将 k-means 中心点放在对最终损失更敏感的值附近，而不是对所有权重值一视同仁，为了确定更敏感的值，我们进行了泰勒扩展，以分析损失是如何随权重 W 的扰动而变化的。
$$
L(W_Q) \approx L(W) - g^\top (W - W_Q) + \frac{1}{2} (W - W_Q)^\top H (W - W_Q)
$$
$g$ 是梯度，$H$ 是W损失的海森矩阵。模型收敛的话，可以认为$g $ 等于0
$$
Q(w)^* = \arg \min_{Q} (W - W_Q)^\top H (W - W_Q)
$$
量化后每个权重的扰动是由二阶导数引入的比例因子加权得出，这凸显了对 Hessian 值较大的权重最小化扰动的重要性，因为它们对最终输出的整体扰动影响更大。换句话说，二阶导数可以衡量每个权重值的重要性。

由于计算 Hessian 的成本较高，使用基于费雪信息矩阵 F 的 Hessian 近似值、可通过样本数据集 D 计算得出。为了提高可行性，我们进一步将费舍尔信息矩阵近似为对角矩阵，假定交叉权重的相互作用可以忽略不计。这样，我们的目标就简化为
$$
Q(w)^* \sim \arg \min_Q (W - W_Q)^\top \text{diag}(\mathcal{F})(W - W_Q)
$$
结果就是，在加权 K 均值聚类设置中，中心点会被拉近到这些敏感的权重值。

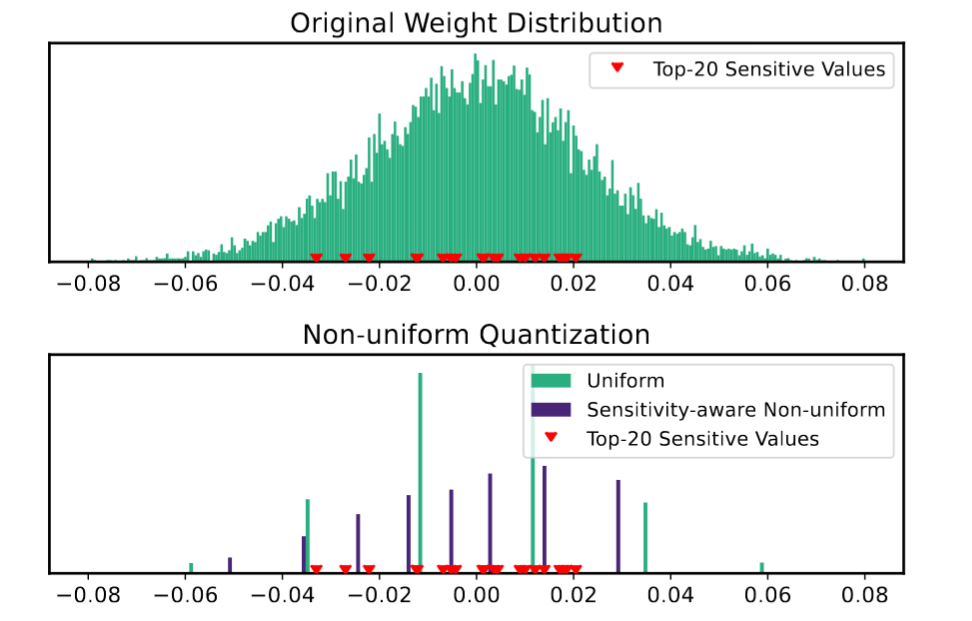
image-20241105192156518

上面是原始分布，以及20个敏感值，下面图，绿色是线性量化，紫色是基于敏感值的非线性量化。

可以看出基于敏感值的非线性量化，能更好的与敏感值分布接近。

Dense-and-Sparse Quantization

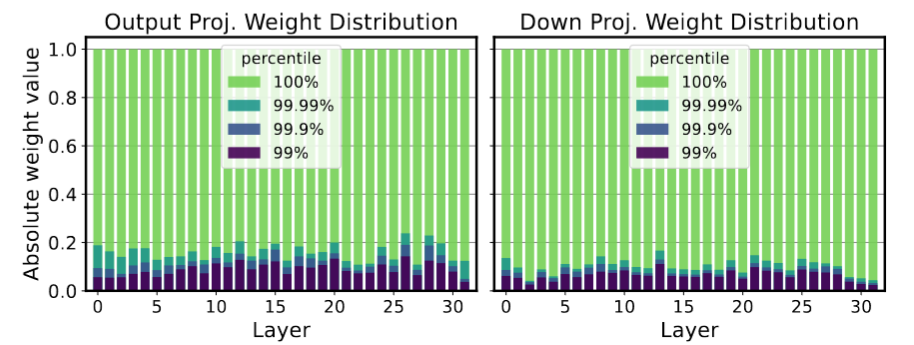
image-20241105192612376

左右分别是 MHA 的输出层和 FFN 的down project输出，可以看出99%的值在很小的分布区间（<10%的区间）

简单地量化大范围的权重会显着降低性能，尤其是在低精度的情况下。只需删除少量异常值，权重值的范围就可以缩小 10 倍，量化分粒度显着提高。而且这将有助于基于敏感值的 k 均值中心集更多地关注敏感值，而不是少数异常值。

于是将权重矩阵根据阈值分为Sparse（也就是包含异常值的部分）和Dense两部分，因为Sparse很少，不会影响推理效率。这些值可以根据 费雪信息矩阵轻松识别。这不仅可以保持 FP16 的异常值以避免它们对模型输出的影响，而且还可以防止方程的质心避免偏向这些异常值。